DH鍵交換とは

2021年11月12日 雑記 ,

0と1の羅列（現代暗号もコンピュータを使います）

この記事では「暗号って何？（公開鍵編）」で触れた鍵交換アルゴリズムの代表「ディフィー・ヘルマン鍵交換」について紹介します。

注：この記事も前回の記事と同様数学的な内容がたっぷり書かれています。

 

DH鍵交換のアルゴリズム

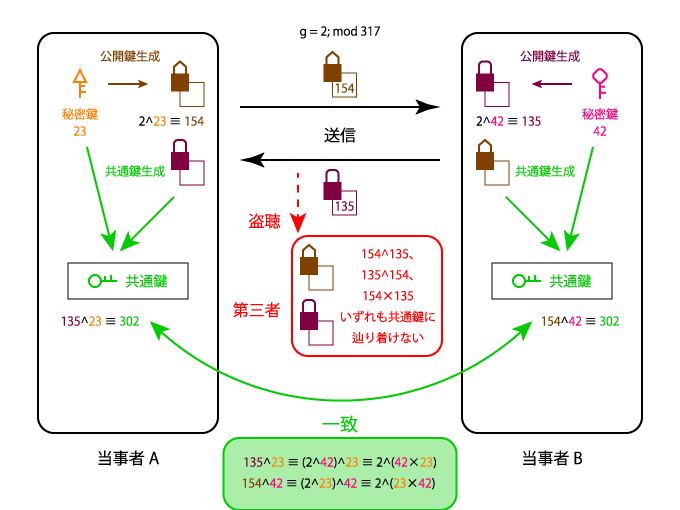
DH鍵交換の仕組み：互いに相手の公開鍵に自分の秘密鍵を作用させることで共通鍵を得る

まず、通信を行う2人の間で自然数gと素数p（これらは公開情報です）を用意します。「gずつかけていったときに、p-1乗で初めて余りが1になる」ように、gとpの組み合わせを選びます。図では、gを2、pを317としていますが、実際はgを2に固定し、素数pには2048ビット等の巨大な素数が使われています。

自分の秘密鍵から生成した値を公開鍵として相手に送信し、互いに相手の公開鍵に自分の秘密鍵を作用させることで共通鍵を得ます。

実際の手順は以下の通りです。

  1. 各自秘密鍵としてその場限りの指数を選ぶ（A: a=23、B: b=42）
  2. 自分が選んだ値をaとして、g^aをpで割った余りを公開鍵として送信する（A: 2^23 ≡ 154、B: 2^42 ≡ 135）
  3. 相手から送られてきた値をCとして、C^aをpで割った余りを計算すると（K_ab: 135^23 ≡ 154^42 ≡ 2^(23×42) ≡ 302）
  4. それぞれ生成した数字は一致し、二者の共通鍵となる

 

DH鍵交換の安全性

このアルゴリズムには、以下の安全性があります。

  • 公開鍵を掛け合わせたり、公開鍵の片方を指数にしたりしても、共通鍵にたどり着けない（154×135、154^135、135^154を計算しても無意味）
  • 指数から余り（2^23や2^42を317で割った余り）を求めるのは簡単だが、逆に余りから指数（2^a ≡ 154や2^b ≡ 135を満たすaやb）を求めるのは困難（離散対数問題）

加えて、秘密鍵や生成した共通鍵を使い捨てにすることで、鍵が破られても過去のセッションで生成・使用した鍵は影響を受けずに済みます（前方秘匿性）。
（RSA暗号を鍵生成に使う場合は同じ公開鍵・秘密鍵を何度も使うことが想定されますので、秘密鍵が破られれば過去に生成した暗号（すなわち共通鍵）まで遡って破られてしまいます。）

指数から余りを求めるのが簡…単…？
さすがにそのまま指数計算するには桁が大きすぎますので、以下のように、「奇数から1を引いて、再び奇数になるまで2で割り続ける」ことで指数を小さくしていきます。

例えば、mod 317として、

  1. g^42 = g^(21×2) = (g^21)^2
  2. g^21 = g^(5×2^2+1) = (((g^5)^2)^2)×g
  3. g^5 = g^(2^2+1) = ((g^2)^2)×g
  4. 2^5 = 32
  5. 2^21 = (((2^5)^2)^2)×2 ≡((32^2)^2)×2 ≡ (73^2)×2 ≡ 257×2 ≡ 197
  6. 2^42 = (2^21)^2 ≡ 197^2 ≡ 135

となります。

或いは、「2乗して余りを求める」ことを繰り返すことでg^(2^k)を順次求めていく方法もあります。

  1. g^42 = g^(2^5 + 2^3 + 2) = (g^(2^5))×(g^(2^3))×(g^2)
  2. 2^2 = 4
  3. 2^(2^3) = ((2^2)^2)^2 = (4^2)^2 = 16^2 = 256
  4. 2^(2^5) = ((2^(2^3))^2)^2 = (256^2)^2 ≡ 234^2 ≡ 232
  5. 2^42 = (2^(2^5))×(2^(2^3))×(2^2) ≡232×256×4 ≡ 135

としても計算できます。

 

DH鍵交換の弱点

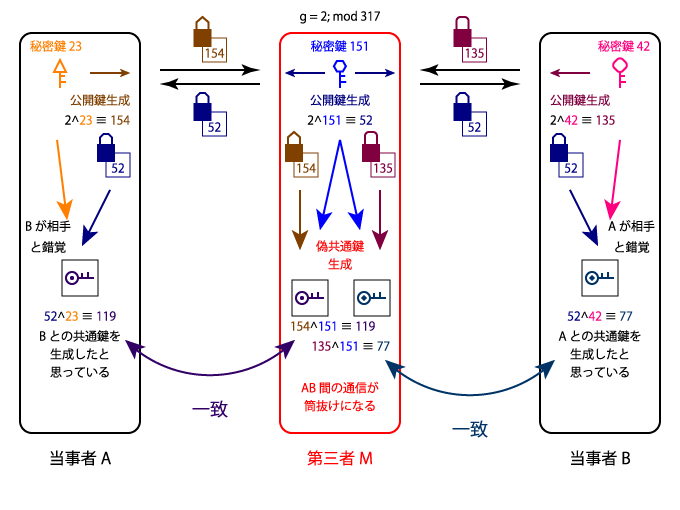
攻撃者は二人のそれぞれの通信相手になりすまし、偽の公開鍵を送り付けることで共通鍵を得る

このアルゴリズムだけでは、中間者攻撃に弱いという欠点があります。

中間者攻撃は、能動的な盗聴方法の一つである。攻撃者が犠牲者と独立した通信経路を確立し、犠牲者間のメッセージを中継し、実際には全ての会話が攻撃者によって制御されているときに、犠牲者にはプライベートな接続で直接対話していると思わせる。中間者攻撃

第三者が、二者の通信経路に割り込み、自分の秘密鍵を用意し、それぞれに対し、本来の通信相手になりすまして鍵交換を行います。それにより、二者に気づかれることなく、共通鍵を手に入れることができてしまいます。

具体的には以下の手順です。

  1. 第三者Mが、秘密鍵としてその場限りの指数を選ぶ（M: m=151）
  2. 二者に対し、それぞれの本来の通信相手の公開鍵と偽り、自分の公開鍵を送信する（M: 2^151 ≡ 52）
  3. 二者から送られてきた公開鍵と自分の秘密鍵から共通鍵を生成する（K_am: 52^23 ≡ 154^151 ≡ 2^(23×151) ≡ 119、K_bm: 52^42 ≡ 135^151 ≡ 2^(42×151) ≡ 77）
  4. 二者は共通鍵を手に入れたと思っているが、実際は第三者との共通鍵であり、以降の通信は筒抜けになる

このため、実際にこの鍵交換を行うには、RSA署名のような認証手段が必須となっております。DH鍵交換とRSA署名を組み合わせることで、それぞれのアルゴリズムの欠点を補完し合っているともいえます。

 

終わりに

以上のように、今日の通信で使われる暗号について若干の説明をさせていただきました。こうして安心してインターネットにつなぐことができるのも、先人たちの賜物ですね！