
今回のクイズ1
「442, 1982, 911, 442, 400, 911, 442」をそれぞれ257乗して2021で割った余りを以下の規則に従ってアルファベットにしてみましょう。
A=260、B=264、C=268、…、Z=360
どんな文字列になりましたか?
RSA暗号方式について解説
注:この文章には数学的な内容がたっぷり書かれています。手っ取り早く答えをご覧になりたい方は下までスクロールしてください。
さて、冒頭の問題を解説するために、RSA暗号/署名について詳しく説明してみましょう。
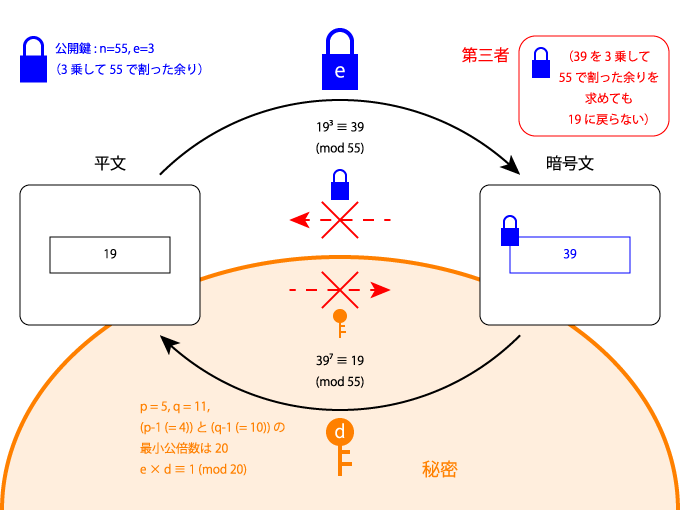
素数p,q(図では5, 11)を秘密裏に用意し、積をn(5×11 = 55)とします。
公開鍵eと秘密鍵dを、e×d-1がp-1でもq-1でも割り切れるように選択します。
(e = 3, d= 7とすれば、3×7 = 4×5 + 1 = 10×2 + 1)
nとeが公開鍵となります。p, q, dは秘密のままです。
C ≡ M^e (mod n) で暗号化、M ≡ C^d (mod n)で平文に戻します。
(「N mod n」で「Nをnで割った余り」を表しています。)
これはフェルマーの小定理を使っています。
(M^e)^d = M^(ed) = M^(xφ+1) ≡ M (mod n) (φはp-1とq-1の最小公倍数)
なお、Mがpの倍数であったとしても、M^(ed) ≡ 0 (mod p)、なおかつM^(ed) = M^(y(q-1)+1) ≡ M (mod q)が成り立ちますので、0 ≦ r < n の条件下で、r ≡ 0 (mod p)かつr ≡ M (mod q)を満たすrはMしかありません。
暗号鍵を使って暗号を作るのと、復号鍵を使って平文に戻すのは互いに逆の操作ですが、用途によってどちらを公開するかが違います。
実際に19をこの方法で暗号化すると19^3 ≡39となり、逆に39^7 ≡19となります。一方、暗号「39」と暗号鍵「3」からは平文「19」を作れませんし、平文「19」と復号鍵「7」からは暗号「39」を作れません。
2つの素数pとqを掛け算するのは簡単ですが、公開鍵nとeから秘密鍵dを求めるには、nをpとqに素因数分解しなければならず、より手間がかかります。これらの計算の手間の非対称性が、公開鍵暗号であることの根拠なのです。
なお、実際の利用時は暗号化前にパディング(例:OAEP)を施し、暗号の解読をより困難なものとしています。
RSA署名と、RSA暗号との関係
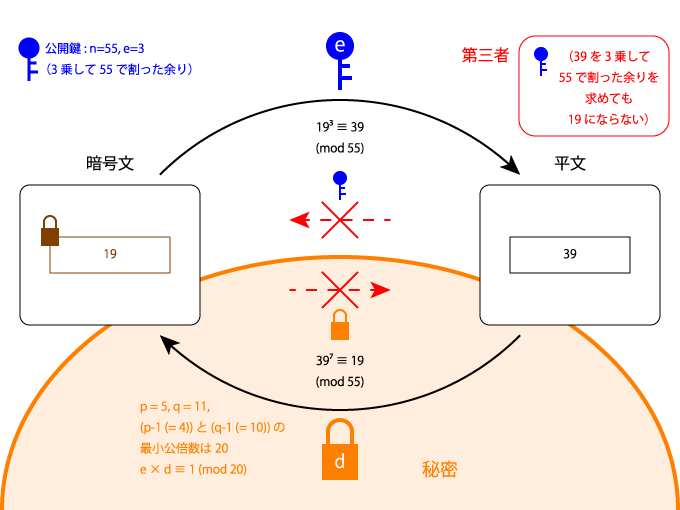
RSA署名は秘密鍵で暗号化する方式を取っていますが、RSA暗号の復号鍵(秘密)を使って署名を生成している、と解釈することもできます。
M ≡ C^d (mod n)で署名値を生成し、C ≡ M^e (mod n) で検証を行います。
クイズ1の答え
さて、冒頭の問題ですが、「ITAISAI」になったでしょうか?(ドラッグすると出てきます)ここまではWindowsの関数電卓で計算できますね?
手計算なら「2乗して2021で割った余りを求める」を8回やって、元の数字を掛けて2021で割った余りを求めることになります。
C^257 = C^(2^8+1) = ((((((((C^2)^2)^2)^2)^2)^2)^2)^2)×C
今回のクイズ2
さて、ここからは秘密鍵を求める問題です。
さて、暗号「442, 1982, 911, 442, 400, 911, 442」を作るのに、元の数字を何乗したでしょうか?
これが解けたら「BLOG」「JAPAN」を同じ方法で暗号化してみましょう。
今回は「2021」という4桁の合成数を使っているため、人力でも素因数分解をして秘密鍵を求めることはできますが、実際はもっと大きい整数が使われています。鍵長が2048ビット(2^2048 ≒ 3.2×10^616)ともなれば、今日のコンピュータでも解読は困難なものとなっております。

